1️⃣ 선형 회귀란?
선형 회귀(Linear Regression)는 입력 변수(독립 변수, X)와 출력 변수(종속 변수, Y) 사이의 관계를 직선 형태로 모델링하는 대표적인 지도 학습 알고리즘입니다.
복잡한 모델로 가기 전, 데이터를 예측하는 가장 기초적인 접근 방식으로 많이 사용됩니다.
예를 들어,
- 공부 시간(X)과 시험 점수(Y)
- 광고 비용(X)과 매출(Y)
- 주택 크기(X)와 가격(Y)
이러한 관계를 하나의 직선(또는 다차원의 평면)으로 표현하고자 할 때 선형 회귀가 활용됩니다.
2️⃣ 선형 회귀의 수학적 구조
📌 단순 선형 회귀
단 하나의 입력 변수 X가 있는 경우, 선형 회귀는 아래와 같은 1차 함수 형태를 가집니다:
Y=WX+b
- Y: 예측값 (종속 변수)
- X: 입력값 (독립 변수)
- W: 기울기 (가중치)
- b: 절편 (bias)
📌 다중 선형 회귀
입력 변수가 여러 개일 경우에는 다음과 같은 수식으로 일반화됩니다:
Y=W1X1+W2X2+⋯+WnXn+b
각 입력 변수에 고유의 가중치 𝑊𝑖를 곱한 후, 이들을 모두 더하고 절편 𝑏를 더해 예측값을 계산한다.
3️⃣ 비용 함수 (Loss Function)
선형 회귀는 예측값과 실제값의 차이를 최소화하는 직선을 찾는 것이 핵심이다.
이 차이를 수치로 표현한 것이 비용 함수(Loss Function)이고, 그중 가장 대표적인 것이 평균제곱오차(MSE)다.
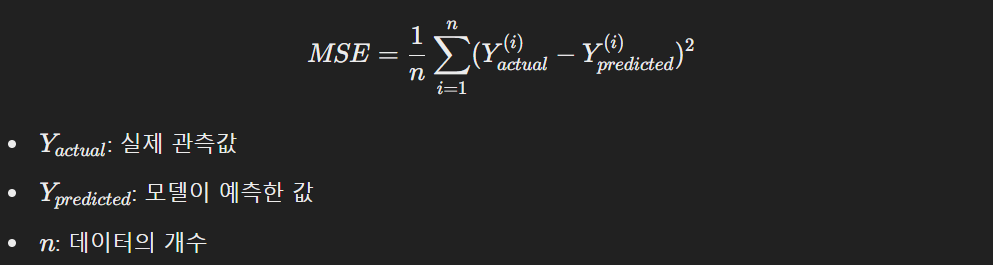
값이 작을수록 예측이 잘 된 것이다.
4️⃣ 경사 하강법 (Gradient Descent)
선형 회귀는 비용 함수를 최소화하는 방향으로 W와 b를 계속 업데이트합니다.
이때 사용하는 알고리즘이 바로 경사 하강법(Gradient Descent)입니다.
업데이트 식은 다음과 같다:

너무 크게 이동하면 발산하고, 너무 작게 이동하면 수렴이 느려지므로 적절한 α\alpha 선택이 중요합니다.
✅ 실습 과제: 직접 선형 회귀 모델 만들어보기
아래 코드를 실행해 실제로 선형 회귀 모델을 만들어보고 시각화까지 해봅시다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 데이터 생성
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1) # 실제 값 (노이즈 포함)
# 모델 학습
model = LinearRegression()
model.fit(X, y)
# 예측값 생성
X_new = np.array([[0], [2]])
y_pred = model.predict(X_new)
# 시각화
plt.scatter(X, y, color="blue", label="Actual Data")
plt.plot(X_new, y_pred, color="red", linewidth=2, label="Predicted Line")
plt.xlabel("X")
plt.ylabel("Y")
plt.legend()
plt.show()📝 결과 해석
- 파란 점: 실제 데이터
- 빨간 선: 모델이 예측한 선형 회귀선
직선이 데이터의 분포를 잘 설명할수록 모델의 예측 성능이 좋다는 의미입니다.
'인공지능 (AI) > 머신러닝 (ML)' 카테고리의 다른 글
| 6 - 숫자부터 문자까지, 분류의 확장: 다중 클래스 분류와 소프트맥스 회귀 (0) | 2025.04.03 |
|---|---|
| 5 - 분류의 시작: 로지스틱 회귀와 시그모이드 함수 (0) | 2025.04.03 |
| 4 - 회귀 모델 성능, 어떻게 더 좋게 만들 수 있을까? (0) | 2025.04.03 |
| 3 - 예측을 더 정밀하게: 다중 선형 회귀 (0) | 2025.04.03 |
| 1 - 데이터가 스스로 배우는 세상: 머신러닝 개요 (0) | 2025.04.03 |
